差分
差分是前缀和的逆运算,主要用于高效地对数组的某个区间进行批量增减操作。 差分的核心思想是通过差分数组/矩阵的端点操作,将复杂操作的时间复杂度从O(n)降至O(1)。
一维差分
实现原理
对于数组arr,构建一个差分数组,其中:
diff[0] = arr[0]diff[i] = arr[i] - arr[i-1],其中i >= 1
通过差分数组,可以快速对数组某个区间进行增减操作:
- 对区间[l, r]的每个元素增加val:
diff[l] += val,diff[r+1] -= val - 对区间[l, r]的每个元素减少val:
diff[l] -= val,diff[r+1] += val
然后通过前缀和运算可以还原出修改后的数组。
代码实现
// 构建差分数组 function buildDiffArray(arr) { const n = arr.length; const diff = new Array(n).fill(0); diff[0] = arr[0]; for (let i = 1; i < n; i++) { diff[i] = arr[i] - arr[i - 1]; } return diff; } // 对区间 [l, r] 增加 val function rangeAdd(diff, l, r, val) { diff[l] += val; if (r + 1 < diff.length) { diff[r + 1] -= val; } } // 从差分数组还原原数组 function restoreArray(diff) { const n = diff.length; const arr = new Array(n); arr[0] = diff[0]; for (let i = 1; i < n; i++) { arr[i] = arr[i - 1] + diff[i]; } return arr; } // 示例 const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]; const diff = buildDiffArray(arr); console.log("差分数组:", diff); // [1, 1, 1, 1, 1, 1, 1, 1, 1, 1] // 对区间 [2, 5] 增加 2 rangeAdd(diff, 2, 5, 2); // [1, 1, 3, 1, 1, 1, -1, 1, 1, 1] const modifiedArr = restoreArray(diff); console.log("修改后的数组:", modifiedArr); // [1, 2, 5, 6, 7, 8, 7, 8, 9, 10]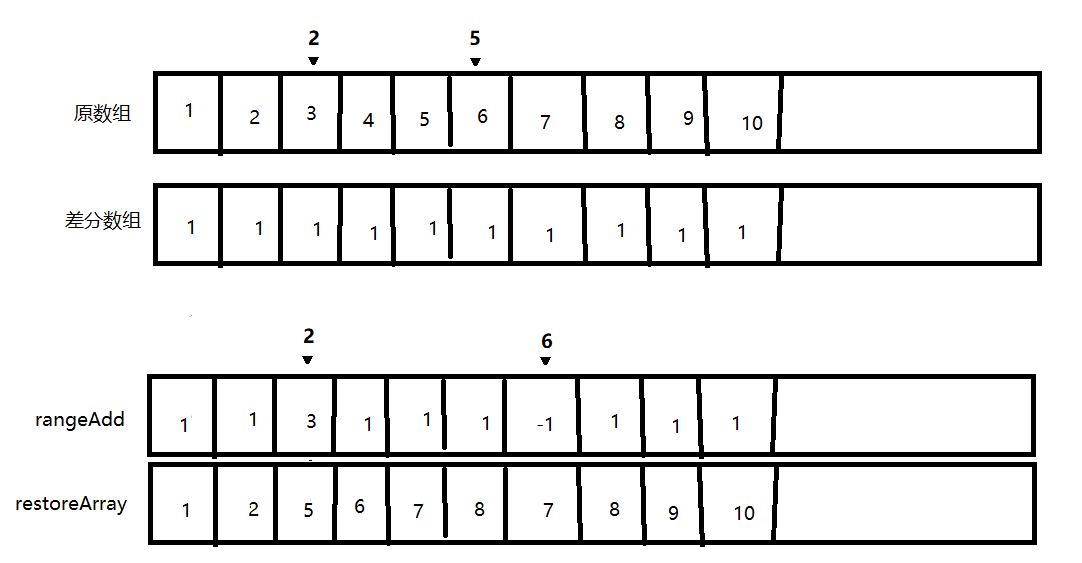
差分图解复杂度分析
- 时间复杂度
- 预处理:
O(n) - 查询:
O(1)
- 预处理:
- 空间复杂度:
O(n)
- 时间复杂度
二维差分
M-原始数组, D-差分数组
预处理:
D[i][j] = M[i][j] - M[i-1][j] - M[i][j-1] + M[i-1][j-1]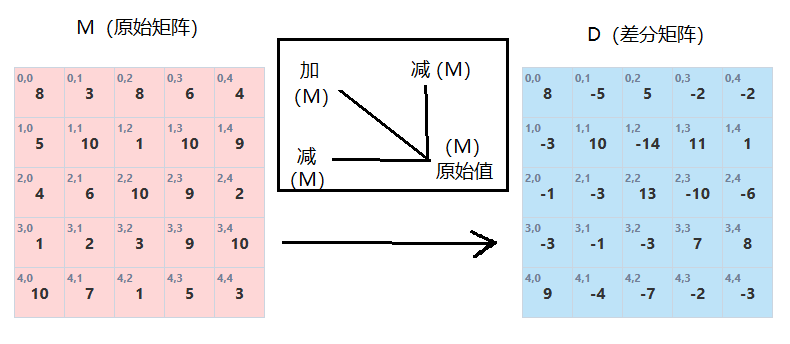
二维差分矩阵图解修改:对(r1,c1)到(r2,c2)区域增加value
D[r1][c1] += valueD[r1][c2+1] -= valueD[r2+1][c1] -= valueD[r2+1][c2+1] += value
代码实现
// 生成随机矩阵
function generateRandomMatrix(size, maxValue) {
const matrix = [];
for (let i = 0; i < size; i++) {
const row = [];
for (let j = 0; j < size; j++) {
row.push(Math.floor(Math.random() * maxValue) + 1);
}
matrix.push(row);
}
return matrix;
}
// 构建二维差分矩阵
function buildDiffMatrix(matrix) {
const n = matrix.length;
const m = matrix[0].length;
const diff = Array(n).fill().map(() => Array(m).fill(0));
// 根据原始矩阵计算差分矩阵
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
diff[i][j] = matrix[i][j];
if (i > 0) diff[i][j] -= matrix[i-1][j];
if (j > 0) diff[i][j] -= matrix[i][j-1];
if (i > 0 && j > 0) diff[i][j] += matrix[i-1][j-1];
}
}
return diff;
}
// 从差分矩阵还原原始矩阵
function restoreMatrixFromDiff(diff) {
const n = diff.length;
const m = diff[0].length;
const matrix = Array(n).fill().map(() => Array(m).fill(0));
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
matrix[i][j] = diff[i][j];
if (i > 0) matrix[i][j] += matrix[i-1][j];
if (j > 0) matrix[i][j] += matrix[i][j-1];
if (i > 0 && j > 0) matrix[i][j] -= matrix[i-1][j-1];
}
}
return matrix;
}
const matrixSize = 5;
const matrix = generateRandomMatrix(matrixSize, 10);
console.log("原始矩阵:", matrix);
const diffMatrix = buildDiffMatrix(matrix);
console.log("差分矩阵:", diffMatrix);
const r1 = 1, c1 = 1, r2 = 3, c2 = 3;
const value = 5
console.log(`对区域 (${r1},${c1}) 到 (${r2},${c2}) 增加: ${value}`);
// 应用差分修改
diffMatrix[r1][c1] += value;
if (c2 + 1 < matrixSize) {
diffMatrix[r1][c2 + 1] -= value;
}
if (r2 + 1 < matrixSize) {
diffMatrix[r2 + 1][c1] -= value;
}
if (r2 + 1 < matrixSize && c2 + 1 < matrixSize) {
diffMatrix[r2 + 1][c2 + 1] += value;
}
const modifiedMatrix = restoreMatrixFromDiff(diffMatrix);
console.log("修改后的矩阵:", modifiedMatrix);